Matematikus Ön? Megmutatjuk, miből számolta ki a Fidesz a választási trükkjeit

Láthattuk az elmúlt 15 évben, hogy a Fidesz célja elsősorban nem az, hogy a magyarok érdekeit szolgálja, hanem a hatalmon maradás. Ezt több intézkedésük is világosan mutatja, például a választási törvény módosításai, valamint az ellenzék számára a médiajelenlét korlátozása, akadályozása. Ebben a cikkben azt tárgyaljuk, hogy bizonyos választási rendszerekben mindig előfordul valamilyen torzítás vagy igazságtalanság, ami lehetőséget ad a manipulációra – és ez matematikailag is bizonyított. Orbán Viktor pártja pedig előszeretettel él a befolyásolásra való eszközökkel.

Először tárgyalunk néhány elterjedt szavazási formát, valamint ezek hiányosságait, hátrányait. Természetesen nem csak a politikai vezetők megválasztására érvényesek az itt bemutatottak – lehet szó akár arról is, hogy mi legyen a program egy csapatépítőn, mikor legyen egy megbeszélés időpontja, vagy bármi másról, aminek egy társaságnak döntenie kell. Ezáltal a példákat sem egy teljes több milliós népességre mutatjuk be, hiszen néhány fő is elég ahhoz, hogy szemléltetni tudjuk a kulcsfontosságú pontokat. A példákban használt színek csak a megkülönböztetést szolgálják, semmilyen összefüggésben nincsenek a valós pártok által használt színekkel.

Egyszerű többség: kézenfekvő, de hemzseg a hibáktól

Tekintsük először az egyik legkézenfekvőbb, legkönnyebben megvalósítható választási formát, az egyszerű többségi rendszert. Maga a megközelítés módszertanilag egyértelmű: aki a legtöbb szavazatot szerzi, az nyer. Azt a látszatot kelti, hogy aki a legtöbb szavazatot kapja, az „a nép akaratából” nyer – viszont a rendszer lehetővé teszi, hogy olyan jelölt nyerje a választásokat, akit a nép többsége valójában elutasít.

Vegyünk egy másik hátrányt egy példán keresztül, méghozzá tekintsük a 2000. évi amerikai elnökválasztást: a két fő jelölt George W. Bush (republikánus) és Al Gore (demokrata) volt, de egy harmadik jelölt is képbe került Ralph Nader személyében, aki a Zöld Pártot képviselte. Nézeteiben inkább Gore-hoz állt közelebb, így Gore szavazói közül elvitt egy jelentős hányadot, csökkentve ezzel az esélyeit. Ezáltal Bush – akit a Nader-szavazók egyáltalán nem szerettek volna az elnöki székben – nyerte meg a floridai választókerületet. Ezt a jelenséget nevezik „elrontó effektusnak”, amikor egy harmadik jelölt megosztja az egyik oldal táborát, és ezzel segíti győzelemhez a legkevésbé kedvelt jelöltet.

Ez nem csak abból a szempontból hátrányos, hogy olyan jelölt nyer, akit a többség nem támogat, ugyanis az „elrontó effektus” a manipulációnak is utat tör: a hatalmon lévők titokban támogathatnak egy „ellenzéki” jelöltet, aki csak megosztja az ellenszavazatokat – és így a hatalom kényelmesen hátradőlhet. Másik hozománya ennek, hogy gyakorlatilag bebetonozza a kétpártrendszert.

Fontos megjegyezni, hogy a kétpártrendszer elengedhetetlen kialakulása csak olyan rendszerekre vonatkozik, ahol „a győztes mindent visz”! Mivel a Parlamentben bizonyos támogatottság mellett mandátumot szerezhetnek a kisebb pártok képviselői is, így a rájuk leadott szavazatok nem „vesznek el” – az Országgyűlésben tudnak hangot adni bizonyos problémáknak, és nyomást tudnak gyakorolni a kormányra, ahogy azt a Mi Hazánk is többször sikeresen megtette.

Konkrét példaként tekintsünk 7 fős baráti társaságot, akik egy baráti összejövetelre szeretnének közös programot szervezni. Hárman inkább túrázni mennének, négyen pedig egy közös éttermi étkezés mellett döntenének. Ha a szavazást lebonyolító inkább túrázni menne, akkor manipulálhatja úgy a helyzetet, hogy bevezet egy opciót, ami hasonló az étteremhez, például közös pizzázást. Az alábbi ábra szemlélteti a szavazók preferenciasorrendjét, és a megválasztott programot. Egyszerű többségi rendszerben a szavazóknak csak a ranglistában 1. helyen szereplő opciót van lehetőségük megjelölni, a többit figyelmen kívül hagyjuk.

A kék jelenti a túrázást, a piros az éttermi látogatást. Bal oldalon látszik, hogy egyszerű többségi szavazásnál az étterem nyerne. Jobb oldalon viszont sárga színnel megjelenik a közös pizzázás is, ami megosztja az étkezni kívánókat, így a túrázás nyer – annak ellenére, hogy a társaság többsége nem szeretné.

Láthatjuk tehát, hogy ez a módszer nem feltétlenül tükrözi megfelelően a nép (társaság) akaratát. Politikai választásoknál az egyszerű többségi szavazás a nagyobb pártoknak kedvez, és ellehetetleníti a kisebb pártok érvényesülését.

Kétfordulós és többfordulós rendszer

A kétfordulós választási rendszer azt a célt szolgálja, hogy enyhíti vagy akár megszünteti az „elrontó effektust”. Ebben a rendszerben a választás első körében minden jelölt indulhat, és ha senki nem szerez abszolút többséget (50 százalék plusz 1 szavazat), akkor a két legtöbb szavazatot szerző jelölt egy második fordulóban újra megmérkőzik. Magyarországon a 2014-es választások előtt egy hasonló rendszer működött, ahol a második fordulóba a legjobb három jelölt juthatott be, valamint azok, akik elnyerték a szavazók legalább 15 százalékának támogatását. 

Mivel a Fidesz egy nagy párt, így nekik az egyfordulós egyszerű többségi rendszer jobban kedvezett – ezért a párt hatalma megszilárdítására a kétharmados többségét kihasználva a választási törvényt is ennek megfelelően módosította.

A többfordulós rendszer egy általánosabb változat, ahol minden körben csak egyetlen jelölt esik ki – aki a legkevesebb szavazatot kapta – így azonban a választási folyamat elhúzódhat, főleg akkor, ha sok jelölt van. Ezt kiküszöbölhetjük azzal, ha a választópolgárok egy rangsort állítanak fel a jelöltek között – részben ezért mutattunk az előző ábrán eleve preferenciasorrendet, holott akkor még csak az első helyezett számított. Ebben az esetben, amikor egy jelölt kiesik, minden rá adott szavazat átszáll a választópolgár rangsorában a következő jelöltre. Így nem kell fizikailag újabb fordulókat szervezni, egyszerűsödik az egész folyamat, és a végeredmény gyorsabban megszületik. Az alábbi ábra 14 szavazó és 4 jelölt esetében szemlélteti a módszer működését.

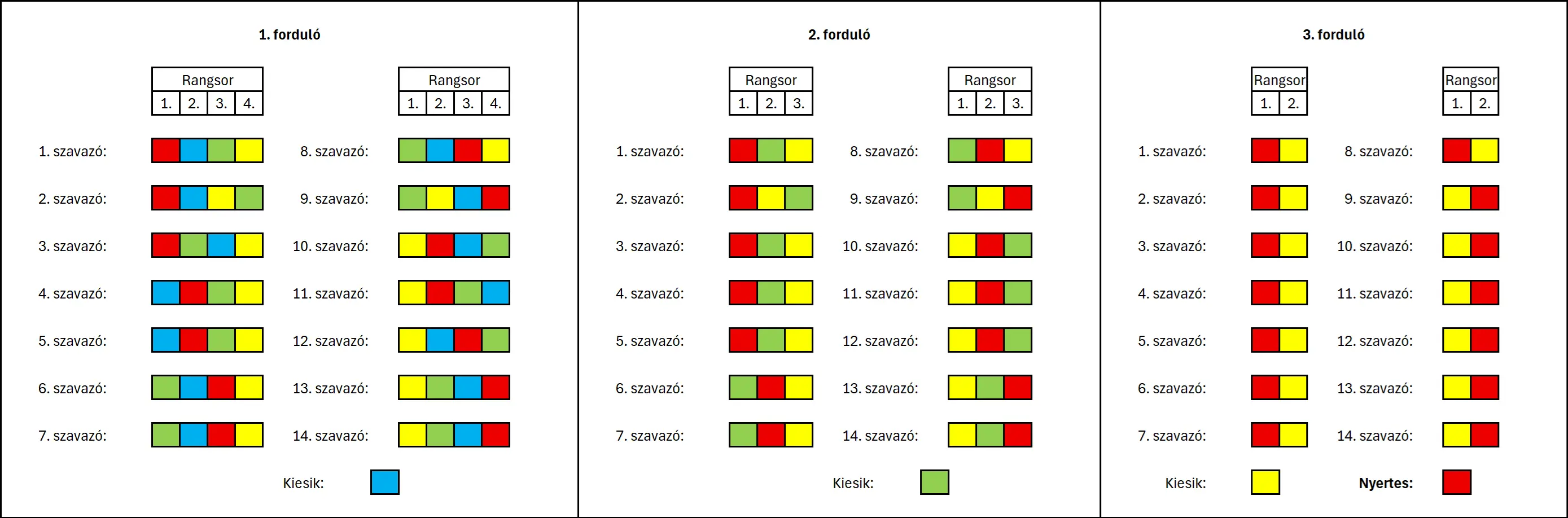
Az első fordulóban a kék kapja a legkevesebb szavazatot, mindössze kettőt, így a 4. és 5. szavazótól átszáll egy-egy szavazat a pirosra.
A második fordulóban a zöld kapja a legkevesebb szavazatot, méghozzá négyet. Tehát három szavazat átszáll a pirosra, egy szavazat a sárgára. Végül a harmadik fordulót a piros megnyeri.

A rendszer legnagyobb előnye, hogy jobban tükrözi a szavazók valódi preferenciáit, hiszen olyan jelölt nyer, akit a legtöbben elfogadhatónak tartanak. Ráadásul a kisebb támogatottságú pártok szavazatai nem vesznek el, azok egy olyan jelöltre szállnak, akit a többiek közül leginkább támogat az adott szavazó. Legnagyobb hátránya azonban, hogy vagy több fordulót kell tartani, ami a választópolgároktól, a szervezőktől és a szavazatszámlálóktól több időt és energiát igényel, vagy pedig maga a voksolás bonyolultabb, mert sorrendet kell felállítani.

Pontozásos módszer

Felmerülhet az ötlet, hogy ha már ranglistát készítenek a szavazók, akkor miért ne pontozhatnánk annak megfelelően, hogy hányadik helyen szerepelnek a listában. Például négy jelölt esetén minden első helyért 3 pont jár a jelöltnek, a második helyezésekért 2 pont, az harmadik helyekért 1 pont, azokért a szavazócédulákért pedig 0 pont, ahol utolsó helyen szerepel. A pontszámokat összesítve kiválaszthatjuk a győztest – nézzük meg ezt az előző példában szereplő 14 szavazóra és négy jelöltre.

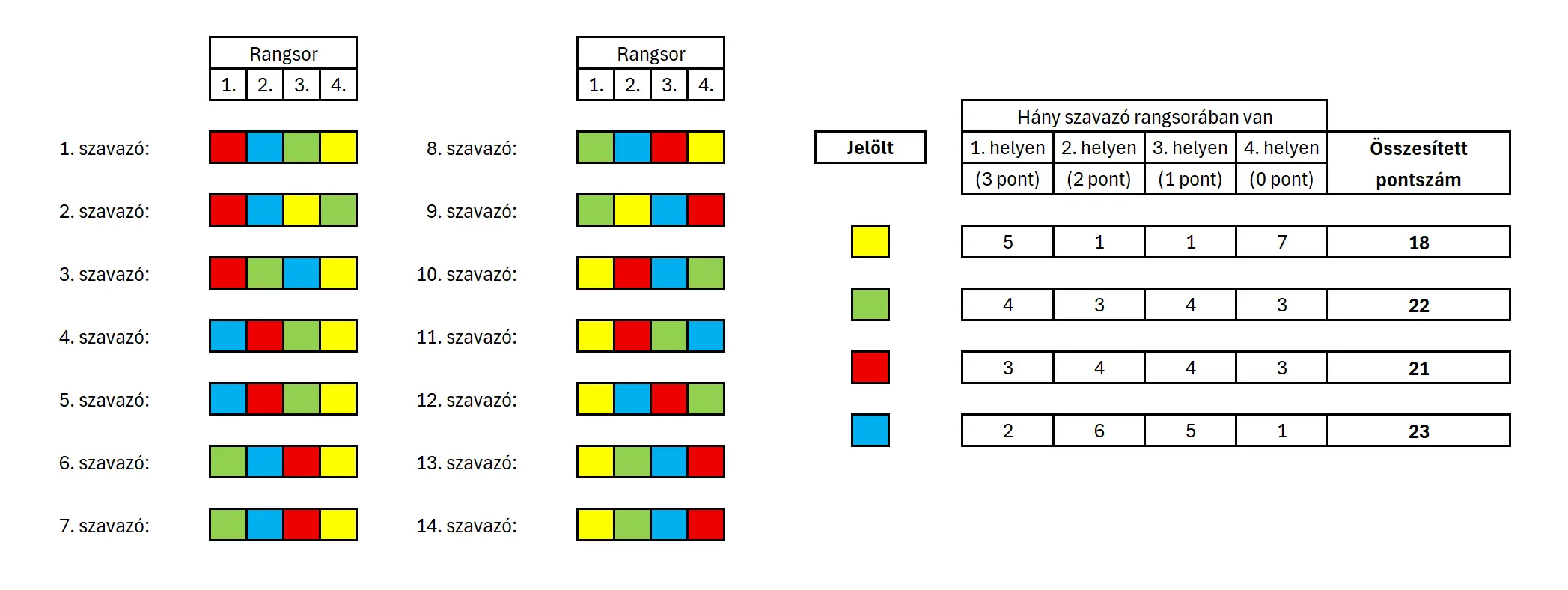
Az összesített pontszámok alapján a kék nyerte a szavazást, pedig csak ketten sorolták első helyre – a többfordulós szavazási módszernél emiatt esett ki elsőként.

A többfordulós módszerhez hasonlóan a pontozásos eljárás is jobban tükrözheti a nép akaratát. Ez a módszer első látásra igazságosnak és demokratikusnak tűnik, hiszen figyelembe veszi a szavazók teljes preferenciarendszerét – ám itt is lehetőség van a manipulációra, amit a következő egyszerű példa szemléltet hat szavazóval és négy jelölttel.

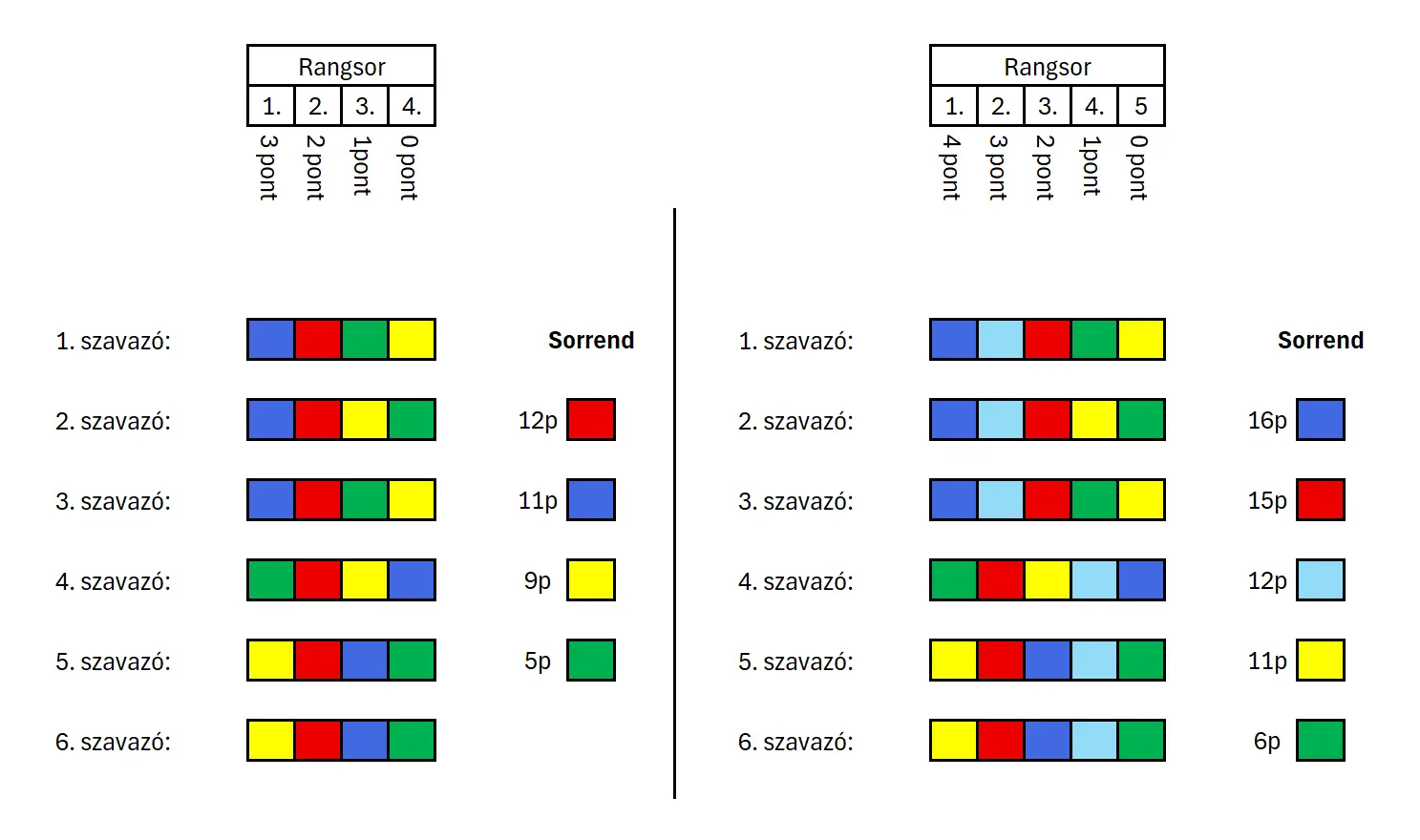
Bal oldalon a pontok összesítése látható a négy jelölt esetén, amit a piros jelölt nyerne.
Jobb oldalon a manipulált rendszer, ahol a kék indít egy hozzá hasonló „kamujelöltet”, aminek következtében a piros hátrébb szorul, így kevesebb pontot kap – ezzel a kék bezsebeli a győzelmet.

A fenti példában épphogy megkaparintja magának a győzelmet a kék jelölt a kamujelölt segítségével. Ha több ilyen áljelölt is indul, akkor a kék pontszámai még jobban megduzzadnak (az első helyezésekért még több pont jár), a pirosat pedig még hátrébb tudja szorítani, így nagyobb lesz köztük a különbség.

Összességében tehát ez a módszer ugyan látszólag igazságosabb, de könnyen a hatalom finom manipulációjának eszközévé válhat.

Most akkor melyiket használjuk?

Négyféle módszert tárgyaltunk (és még van több is), tulajdonképpen mindegyik rangsorolásos: az egyszerű többségi szavazás esetén is feltételezhetjük, hogy van egy preferenciasorrend, de csak az első helyen szereplőt vesszük figyelembe; a kétfordulós esetben pedig az első két helyen szereplőt. Tekintsük a korábbi példát 14 szavazóval és négy jelölttel. Láthattuk, hogy a többfordulós eljárással a piros nyert, a pontszámozásos módszerrel pedig a kék. Nézzük meg, mi a helyzet a másik két esetben is:

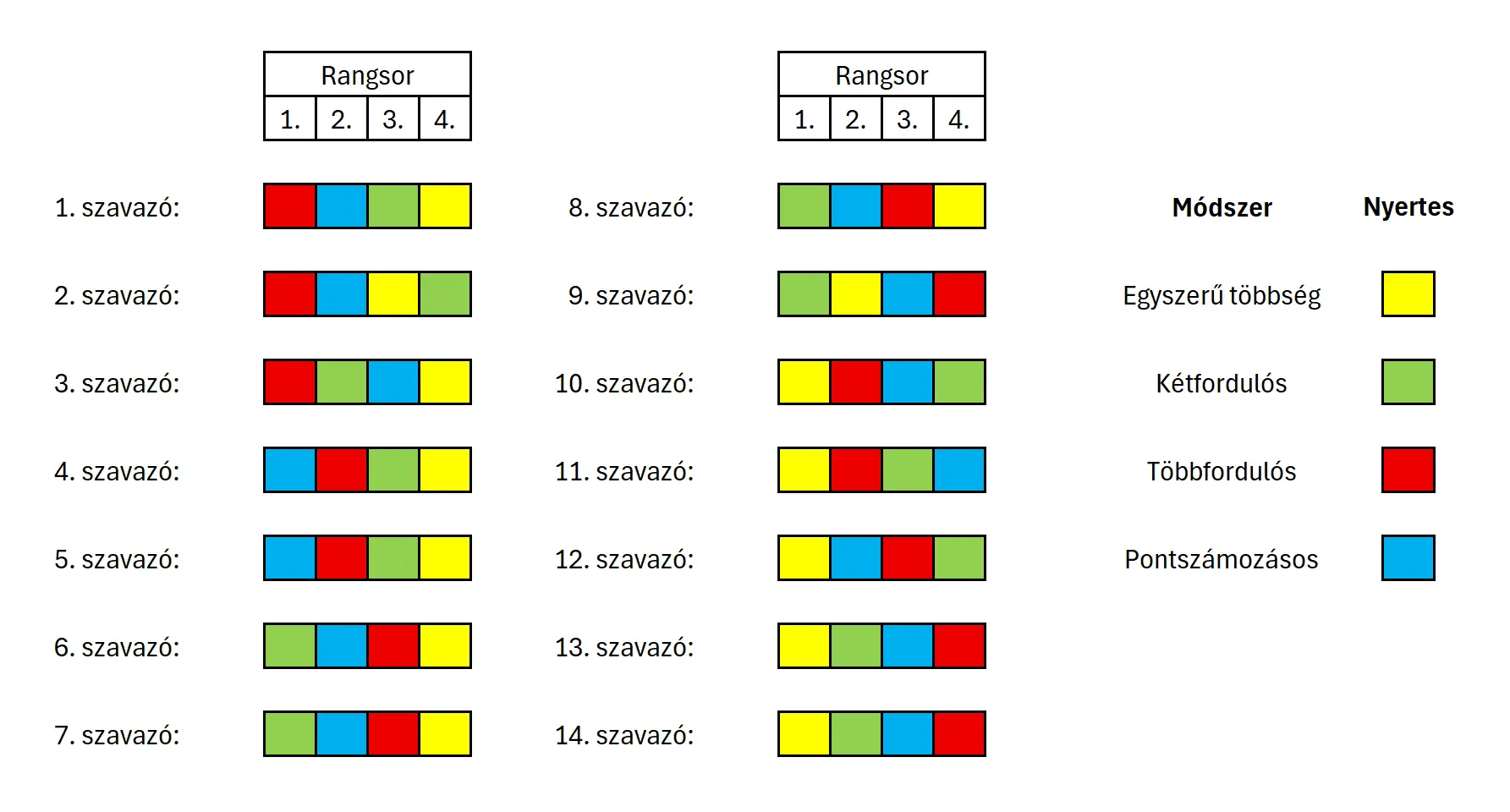
Egyszerű többség esetén a sárga nyer 5 első helyezéssel, kétfordulós esetben pedig a zöld nyer, hiszen ő kapja a kiesők szavazatainak nagy részét.

A négy módszer tehát négy különböző eredményre vezetett egy ilyen kis méretű példa esetén is. Maga a szavazási módszer is rengeteg vitát szülhet abból a szempontból, hogy melyik demokratikusabb, melyik tükrözi a leginkább a nép akaratát. A matematikusok megfogalmaztak néhány feltételt, amelyeket teljesítenie kell egy igazságos rangsorolásos rendszernek – ezeket nézzük át a továbbiakban.

Milyen feltételeknek kellene teljesülni egy „tökéletes” rangsorolásos rendszerben?

Minden választó tehát egy teljes sorrendet állít fel az összes jelöltről, a rendszer célja pedig az, hogy az egyéni sorrendekből kialakítson egy összesített társadalmi sorrendet, amely alapján eldől, ki nyeri a választást, és hogyan alakul a jelöltek végső rangsora. Van három alapvető feltétel, amelyek egyidejű teljesülése elvárás lenne, ha igazságos és torzításmentes rendszert szeretnénk.

Az egyik ilyen az egyhangúság megtartása: ha minden választó egyöntetűen úgy ítéli meg, hogy az A jelölt jobb, mint a B jelölt, akkor az összesített sorrendben is A-nak meg kell előznie B-t – tehát a közös döntésnek is tükröznie kell az egyhangú álláspontot.

A másik fontos feltétel a függetlenség a nem releváns alternatíváktól, aminek tekintetében két jelölt egymáshoz viszonyított helyét csak az határozhatja meg, hogy az egyes szavazók őket hogyan rangsorolják. Tehát ha például az A és B közti (társadalmi) sorrendet szeretnénk eldönteni, akkor semmilyen módon nem befolyásolhatja az eredményt, hogy a szavazók hogyan értékelnek egy harmadik (C) jelöltet, hogy kiesik-e egy másik jelölt a versenyből, vagy hogy bekerül-e egy új jelölt. Láthattuk a fenti példákból, hogy az egyszerű többségi rendszerben ez nem teljesül – az új opció megosztotta a szavazatokat, ezáltal egy kevésbé kedvelt lehetőség nyert. Továbbá azt is szemléltettük, hogy a pontszámos rendszer sem teljesíti ezt a feltételt, hiszen a „kamujelölt” bevonása megváltoztatta a végeredményt.

Végül a harmadik feltétel, hogy a rendszer legyen diktatúramentes, tehát a végső rangsor ne egy adott szavazó preferenciasorrendjének másolata legyen.

A nagy leleplezés: nem teljesülhet mindhárom egyszerre

A fenti három feltételezés észszerűnek tűnik ugyan, azonban van egy bökkenő: matematikailag bizonyított, hogy a három feltétel nem teljesülhet egyszerre egyetlen rangsorolásos választási módszerben sem. Ez azt jelenti, hogy

az egyetlen olyan rendszer, ami teljesíti az egyhangúság megtartását és a nem releváns alternatíváktól való függetlenséget is, az a demokrácia totális ellentéte, a diktatúra.

Nem ennyire disztópikus a helyzet azonban – hiszen ennek az elemzésnek vannak korlátai.

A modell korlátai

Fontos hangsúlyozni, hogy a lehetetlenségi tétel csak a rangsorolásos választási rendszerekre vonatkozik. Nem érvényes azokra az eljárásokra, ahol a szavazók nem sorrendet állítanak, hanem például 10-es skálán pontozzák a jelölteket, és több jelölt is kaphatja ugyanazt a pontszámot. Ezekben a rendszerekben nem alakul ki egyértelmű preferenciasorrend, amit feltételeztünk korábban. Hasonlóan nem érvényes arra a szavazási modellre sem, amikor a választópolgárok szimplán bejelölik, hogy mely jelölteket hagyják jóvá – akár többet is.

A rangsorolásos választások esetén az egyik leglényegesebb korlát a gyakorlati kivitelezhetőség. Minél bonyolultabb a szavazási módszer, annál nagyobb az esély arra, hogy a választók nem értik pontosan a szabályokat, vagy egyszerűen úgy döntenek, hogy nem bajlódnak vele. Ez jelentős mértékben csökkentheti a részvételi arányt, és megnövelheti az érvénytelen szavazatok számát is. Ha sok párt van, azt sem feltétlenül várhatjuk el, hogy a voksolók mindegyikről tisztában legyenek annyira, hogy el tudják helyezni a rangsorba. Felmerül a kérdés, hogy mit csináljanak azokkal, akiket nem ismernek kellőképpen. Tegyék a lista végére? Helyezzék el véletlenszerűen valahova? Ezek mind torzíthatják a végeredményt. Továbbá a fenti leírásban és vizsgálatokban nem tértünk ki a holtversenyek kezelésére sem.

Végül, bármilyen elegáns is legyen a matematikai modell, az nem védi ki a választások manipulálásának egyéb formáit.

Hiába a jól kidolgozott szabályrendszer a választók érdekeinek megfelelő képviseletére, ha a hatalomnak lehetősége van például a választási törvény módosítására, a választókerületek önkényes átrajzolására (más szóval gerrymanderingre), vagy az ellenzék ellehetetlenítésére például a médiajelenlét korlátozásával. 

Emellett sok helyen megjelenhetnek nyílt vagy burkolt retorziók, amelyek elrettentik az embereket a szabad véleménynyilvánítástól.

(Kiemelt kép: Remenyiczki Éva, felhasznált források: Koszticsák Szilárd/MTI, Európai Bizottság, Pexels)